那些可(kě)以用雙指針解決的題目

• 什麼時候用雙指針，該咋用？
• • 雙指針思想
  • • 35.搜索插入位置
    • 27.移除元素
    • 209，長度最小的子(zǐ)數組

什麼時候用雙指針，該咋用？

雙指針思想

雙指針是我們做題中(zhōng)經常用到的思想，所以這個(gè)在刷題初期是一定要會的。其實我們早就學習過這個(gè)方法，我們通(tōng)過二分查找來描述一下(xià)這個(gè)思想。

二分查找首先定義兩個(gè)指針，左指針和(hé)右指針，分别指向數組的頭和(hé)尾，然後計算出他倆的中(zhōng)間的索引，其值和(hé)目标值進行比較，如(rú)果目标值更大則說明目标值在中(zhōng)間索引和(hé)右指針中(zhōng)間，則需要移動(dòng)左指針到中(zhōng)間索引的後一位。如(rú)果目标值比中(zhōng)間值小，則需要移動(dòng)右指針到中(zhōng)間索引的前一位。不斷執行，直至找到目标值，或當該數組不含有目标值，左指針和(hé)右指針重合時跳出該循環。

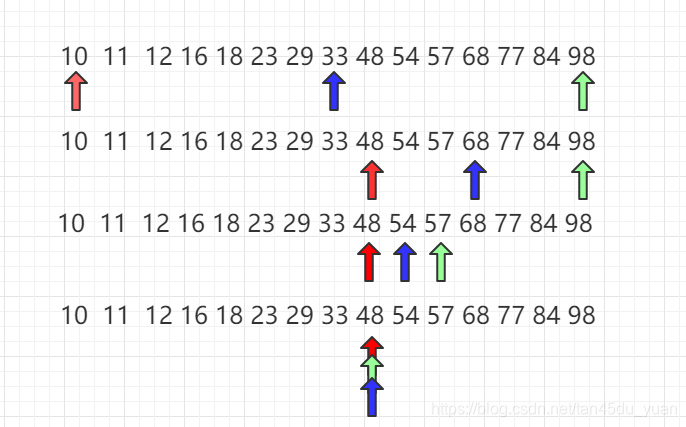
二分查找代碼

 public static int halfnum(int[] arraynum ,int b){
            int hi =arraynum.length-1;
            int lo = 0;
            //先判斷數組是不是空
            if (arraynum.length==0){
                return -1;
            }            
            while(hi>=lo){
                 //判斷是否等于要猜的數
                if(b==arraynum[(hi+lo)/2]){
                    return (hi+lo)/2;
                }
                //大于中(zhōng)間數的情況
                else if (b>arraynum[(hi+lo)/2]){
                    lo= (hi+lo)/2+1;
                }
                //小于中(zhōng)間數的情況
                else{
                    hi=(hi+lo)/2-1;
                }
            }
           return -1;
        }

35.搜索插入位置

給定一個(gè)排序數組和(hé)一個(gè)目标值，在數組中(zhōng)找到目标值，并返回其索引。如(rú)果目标值不存在于數組中(zhōng)，返回它将會被按順序插入的位置。你(nǐ)可(kě)以假設數組中(zhōng)無重複元素。

示例 1:

輸入: [1,3,5,6], 5
輸出: 2

示例 2:

輸入: [1,3,5,6], 2
輸出: 1

示例 3:

輸入: [1,3,5,6], 7
輸出: 4

示例 4:

輸入: [1,3,5,6], 0
輸出: 0

題目很好理解，但是我們想要一次AC是不太容易的。我們根據題意可(kě)以想到，這樣共有四種可(kě)能

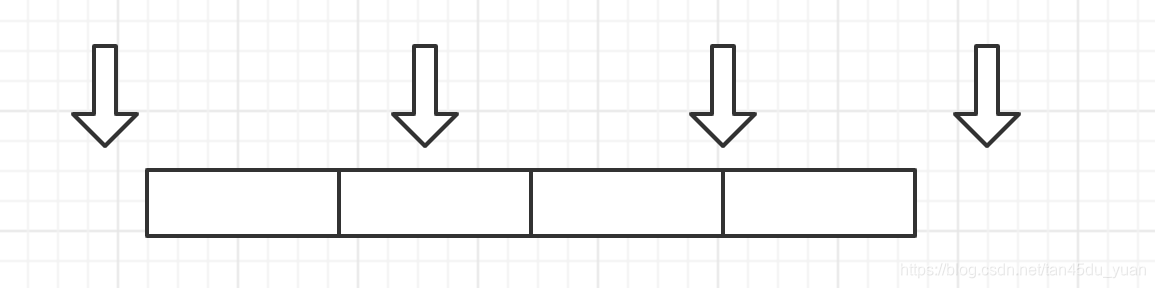
插入情況無非就這幾種

（1）比數組裡的任何值都小，插入頭部

（2）比數組裡的任何值都大，插入尾部

（3）查詢到數組元素，返回該處索引值

（4）數組内無該元素，将其插入兩元素之間。

所以我們可(kě)以通(tōng)過以下(xià)代碼實現該題

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while(left <= right) {
            //中(zhōng)間值，與target對比
            int mid = (left + right) / 2;
            //第三種情況
            if(nums[mid] == target) {
                return mid;
            //移動(dòng)左指針
            } else if(nums[mid] < target) {
                left = mid + 1;
            } else {
                //移動(dòng)右指針
                right = mid - 1;
            }
        }
        //1，2，4三種情況都在循環内部，我們隻需輸出左指針即可(kě)。
        return left;
    }
}

---

剛才我們說了雙指針思想的重要性，下(xià)面這個(gè)題目也是可(kě)以完全通(tōng)過雙指針思想實現的，所以說雙指針的思想是必須有的。你(nǐ)可(kě)以通(tōng)過下(xià)面這個(gè)題目完全體會到雙指針的重要性

27.移除元素

給你(nǐ)一個(gè)數組 nums 和(hé)一個(gè)值 val，你(nǐ)需要 原地 移除所有數值等于 val 的元素，并返回移除後數組的新長度。

不要使用額外的數組空間，你(nǐ)必須僅使用 O(1) 額外空間并 原地 修改輸入數組。

元素的順序可(kě)以改變。你(nǐ)不需要考慮數組中(zhōng)超出新長度後面的元素。

示例 1:

給定 nums = [3,2,2,3], val = 3,

函數應該返回新的長度 2, 并且 nums 中(zhōng)的前兩個(gè)元素均為 2。

你(nǐ)不需要考慮數組中(zhōng)超出新長度後面的元素。

示例 2:

給定 nums = [0,1,2,2,3,0,4,2], val = 2,

函數應該返回新的長度 5, 并且 nums 中(zhōng)的前五個(gè)元素為 0, 1, 3, 0, 4。

注意這五個(gè)元素可(kě)為任意順序。

你(nǐ)不需要考慮數組中(zhōng)超出新長度後面的元素。

該題目我們可(kě)以創建兩個(gè)指針，一前一後，前面的負責探路(lù)後面的負責填充，當前面查詢到需要移除的元素時直接跳過該元素，繼續前進。後面的指針隻負責往該數組裡面填充不需要移除的數字。所以我們可(kě)以根據以下(xià)代碼實現

class Solution {
    public int removeElement(int[] nums, int val) {
    //特殊情況
      if(nums==null){
          return 0;
      }     
      int j = 0;//慢指針，i代表快指針
      for(int i = 0;i<nums.length;i++){
         //正常情況直接賦值給i          
          if(nums[i]!=val){
              nums[j]=nums[i];
              j++;
          }
          //如(rú)果為需要删除的值時，則快指針移動(dòng)，慢指針不動(dòng)。
      }
       return j;
    }
}

---

剛才我們學習了兩個(gè)雙指針的題目，是不是對這個(gè)做題思想有了一些理解了，下(xià)面我們來使用一個(gè)更加高級的雙指針，這個(gè)也是經常使用的思想，但是歸根結底還是雙指針思想。

該題目的思想也是雙指針的思想，不過這個(gè)代碼比較難寫一些，用到的情況也是比較多的，所以我們這個(gè)題目要用心體會一下(xià)。

209，長度最小的子(zǐ)數組

給定一個(gè)含有 n 個(gè)正整數的數組和(hé)一個(gè)正整數 s ，找出該數組中(zhōng)滿足其和(hé) ≥ s 的長度最小的 連續 子(zǐ)數組，并返回其長度。如(rú)果不存在符合條件的子(zǐ)數組，返回 0。

示例：

輸入：s = 7, nums = [2,3,1,2,4,3]
輸出：2
解釋：子(zǐ)數組 [4,3] 是該條件下(xià)的長度最小的子(zǐ)數組

題目含義比較好理解，則是在數組裡面找出長度最小的子(zǐ)數組，子(zǐ)數組的元素和(hé)大于等于目标值。這個(gè)題目我們就用到了滑動(dòng)窗口的思想。

滑動(dòng)窗口：就是通(tōng)過不斷調節子(zǐ)數組的起始位置和(hé)終止位置，進而得到我們想要的結果我們也可(kě)以看成是雙指針的一種。

在該題中(zhōng)，我們可(kě)能遇到這種情況 大家思考一下(xià)，數組的值是1，2，3，4，5我們的s為5，所以我們第一次的子(zǐ)數組（滑動(dòng)窗口）長度則為3，1+2+3>5,這時左指針在1的位置，右指針在3的位置，但是2+3=5同樣符合，所以我們就需要移動(dòng)左指針，此時窗口長度則改為2了。然後我們保留該值，繼續移動(dòng)左指針，判斷3是否仍符合，此時發現不符合了，則需要移動(dòng)右指針，移動(dòng)到下(xià)一個(gè)符合情況的元素，繼續執行剛才的步驟，直到數組的最後。所以整個(gè)過程中(zhōng)滑動(dòng)窗口的長度變化為，3,2,3,2,3,2,1，最小的則為1.

我們可(kě)以通(tōng)過以下(xià)代碼解決該題。

class Solution {
    public int minSubArrayLen(int s, int[] nums) {
        int chiledlen = Integer.MAX_VALUE;
        int winlen = 0;//窗口大小
        int sum = 0;
        int i = 0;//起始長度位置
        for(int j = 0 ; j < nums.length;j++){
              sum += nums[j];
              //發現符合條件的情況
              //循環内部的代碼是精髓所在
              while(sum>=s){
                  winlen = j-i+1;
                  chiledlen = Math.min(chiledlen,winlen);
                  //下(xià)面兩行是滑動(dòng)窗口的意義所在，改變起點位置，判斷是否仍符合條件
                  sum-=nums[i];
                  i++;
              }

        }
        return chiledlen == Integer.MAX_VALUE ? 0:chiledlen;
    }
}

通(tōng)過以上三個(gè)題目我們是不是對雙指針思想有了一些理解了，該思想不僅可(kě)以用在數組的題目上，鍊表同樣适用。所以我們要完全掌握，這三個(gè)題目大家有時間的話還是自己動(dòng)手做一下(xià)。

---